Sir Roger Penrose

(08 de agosto de 1931, Colchester, Inglaterra - )

Por Bronny Sánchez.

Asociación Larense de Astronomía, ALDA.

El autor se pregunta: ¿Cuál es la mejor imagen para representar a Roger Penrose al inicio de esta biografía? Si no adherimos a su estudio de las Teselaciones, figuras que representan líneas, tramas, trazos, simetrías; un rayo de luz, que durante su trayecto, describe la forma de un Twistor, ¿por qué no de igual forma a él? Este maravilloso retrato en carbón, del artista Joens, vemos a Penrose como lo que, en la historia y en la actualidad representa: una figura resaltante.

_____________________________________________________________________________

Al momento de redactar la presente biografía, Penrose se encuentra a solo unos días de sus 89 años, esto es, el 8 de agosto de 2020. Sobre sus hombros, descansa toda una historia de vivencias entre los más reconocidos físicos teóricos, matemáticos y cosmólogos de la historia. Por ende, Penrose representa la esencia de la mayoría de los desarrollos científicos que han dado paso a las más diversas teorías sobre el Universo, teorías que de una u otra forma, siempre llevaran la signatura y aporte de Roger Penrose, una leyenda viva que "hace estragos", como las singularidades que él ayudó a revivir y que a partir de 1965, le dio una completa aplicabilidad y madurez a la Teoría de la Relatividad.

        Roger Penrose nace en Colchester, Essex, Inglaterra, el 8 de Agosto de 1931. Su familia se destaca en diversos ámbitos profesionales. Su padre, era el científico Lionel Penrose, médico genetista, que fue elegido fellow de la Sociedad Real. El estuvo involucrado en un proyecto denominado Sondeo Colchester, el cual llevó a descubrir si factores inherentes o factores de entorno, podría resultar en que una persona sufra de enfermedades mentales.

        Lionel estaba llevando a cabo dicho trabajo, al momento en que Roger nació. Su madre, era Margareth Leathes; su hermano, un físico teórico, Oliver Penrose, quién fue profesor de matemática, primero, en la Universidad Abierta y después, en la Universidad Heriot-Watt, en Edinburgo, Escocia; su otro hermano, el ajedrecista Jonathan Penrose, fue campeón de ajedrez diez veces, entre 1958 y 1969. Muchos argumentan, que fue el más talentoso jugador de ajedrez británico de todos los tiempos.

        En 1939, el padre de Roger se fue a los Estados Unidos con su familia, pero como todo apuntaba al no término de la guerra, decidió no regresar a Inglaterra con su familia, sino que aceptó un cargo en el Hospital Londres, en Ontario, Canadá. Roger asistió a una escuela en Londres, Ontario, pero a pesar de que fue en este periodo en que Roger se interesó por las matemáticas, no fue su escolaridad la que estimuló su interés; más que ello, fue su familia. Roger diría:  

Recuerdo haber hecho varios poliedros cuando tenía diez...

El padre de Roger llegó a ser Director de Investigación Psiquiátrica en el Hospital Londres, Ontario. El hermano de Roger, Oliver, escribió sobre Roger:

... tenía dos años más que yo, pero cuatro años más adelantado en estudios! Sabía muchas cosas sobre matemática a una edad tan temprana y tomó gran interés, tanto en matemática como en física...

Penrose haciendo lo que más le apasiona: su afición por las matemáticas. Aquí aparece mostrando la membrana de un agujero negro. ¿Se puede viajar por el tiempo a través de este y emerger en otro universo? Son estas y otras preguntas que resultan cuando nos adentramos al mundo de la cosmología… Y si… ahí está la singularidad… diría Penrose a los asistentes.

        En 1945, al término de la Segunda Guerra Mundial, la familia Penrose retornó a Inglaterra. El padre de Roger obtuvo un cargo como Profesor de Genética Humana, en la Universidad London College, y Roger asistió a la Universidad Scholl College, en Londres. Su interés en la matemática crecieron, pero su familia veía que Roger seguía los pasos de su padre, inclinándose a una carrera de medicina. Pero, como era típico en las Universidades para la época, la biología y la matemática eran carreras alternativas en la Universidad Scholl College, en la que los estudiantes debían elegir una de las dos actividades. 

... recuerdo una ocasión, cuando tenía que decidir que carrera debía elegir para estudiar los dos últimos años. Cada uno de nosotros fuimos a hablar con el director; uno tras otro, me tocó a mí y me dijo: "Bien, ¿qué carrera escogerás para especializarte el próximo año? Le dije: "Biología, química y matemática" El me dijo: "¡No, eso es imposible! no puedes hacer biología y matemática al mismo tiempo, no tenemos esa opción". Como no quería perder mi deseo en la matemática, le dije: "Matemática, física y química" en ese orden. Mis padres estaban más que enojados cuando regresé a casa; mi carrera médica había desaparecido de un solo golpe...  

        Penrose entró a la Universidad London College, el cual haría sin pagar ningún tributo, ya que su padre era profesor allí. Fue premiado con un grado B.Sc. con Honores de Primera Clase y después de ello, decidí ir a Cambridge para realizar su grado en matemática pura. Roger seguía los pasos de su hermano mayor, Oliver, quién también había estudiado en la Universidad London College y de allí, también se fue a Cambridge para continuar en su carrera de investigación, pero Oliver escogería estudiar Física.

"Cuando nos encontramos por primera vez, hace unos 45 años cuando, como estudiante de investigación en Cambridge, compartí una oficina con varios colegas, uno de los cuales, era Oliver Penrose, hermano mayor de Roger y ahora, una distinguida autoridad en mecánica estadística. Mis intereses de investigación eran también en mecánica estadística, pero cuando cambié mis estudios a relatividad y cosmología a mitad de mis estudios de Ph.D, Oliver me dijo que podría encontrarme con su hermano, "quien piensa geométricamente".

Dennis W. Sciama.

SISSA- ICTP Trieste, Departamento de Física, Universidad de Oxford.

        Roger, sin embargo, se centró en sus estudios de investigaciones matemáticas y, al entrar al St John's College, donde comenzó sus investigaciones en geometría algebraica, siendo supervisado por Hodge. Después de un año de estudios en Cambridge, vió que sus intereses no eran de particular interés a las de Hodge, por lo que cambiaría a su supervisor, en este caso, por John Todd, algebrista y geómetra quién sería el supervisor de su tesis. Penrose obtuvo su Ph.D. por su trabajo "Métodos Tensores en Geometría Algebraica" por la Universidad de Cambridge, en 1957. Pero, para esta epoca, también se había interesado en la física. Roger describiría como los tres cursos que atendió durante su primer año en Cambridge, lo llegaron a influenciar:

...Recuerdo haber asistido a los tres cursos, los cuales, no tenían nada que ver con las investigaciones que, supuestamente, estaba por hacer. Uno, fue el curso dado por Hermann Bondi sobre relatividad general, la cual era fascinante... El otro, por Paul Dirac, sobre mecánica cuántica, que era muy hermosa y dada de una manera diferente... y el tercer curso... era un curso de lógica matemática por Steen. Con él aprendí sobre las máquinas de Alan Turing y los teoremas de Kurt Godel...

        La primera gran influencia que tuvo Roger, lo llevaron a aumentar su interés en física. Era Dennis Sciama, un profesor de física, amigo de su hermano Oliver. Penrose dijo:

(Sciama) tuvo una gran influencia en mí. El me llevó a tener un gran interés en física, y la excitación de moverme a través de esta; el era ese tipo de persona, que convenía a tener el interés de lo que actualmente era la física...

        Mientras trabajaba en Cambridge, comenzó a publicar artículos sobre semigrupos y anillos de matrices. En 1955 publicó "Una inversa generalizada para Matríces" en Proceedings of the Cambridge Philosophical Society, En este trabajo, Penrose definió una inversa generalizada de un complejo rectangular (o posiblemente cuadrado y singular) matriz como solución única a un tipo de ecuaciones. El usó esta inversa generalizada para problemas tales como solventar los sistemas de las ecuaciones en matrices y encontrar un nuevo tipo de decomposición espectral. Su segunda publicación de 1955 fue "Notas sobre semigrupos inversos" publicadas en el mismo boletín, junto con Douglas Munn, como co-autor.

"Roger ha ganado un gran premio para todos nosotros: un profundo entendimiento de la estructura del espacio-tiempo, especialmente, la relación de causalidad entre un punto del espacio-tiempo y otro... probablemente la predicción más importante en relatividad general"

John A. Wheeler.

Físico norteamericano, quién en 1969, acuñó el término Agujero Negro.

        Penrose estuvo en su año académico 1956-57, como Conferencista Asistente en Matemática Pura, en el Bedford College, en Londres, y allí fue asignado como Fellow de Investigaciones en St John's College, en Cambridge. Este fue un post de tres años, y durante su estadía allí, contrae matrimonio con Joan Isabel Wedge, en 1959. Antes de que su membresía como fellow finalizara, Penrose había obtenido una beca de investigación en la OTAN (Organización del Tratado Atlántico Norte o NATO, por sus siglas en inglés) lo que llevó a Penrose a estar los años 1959-61, en los Estados Unidos, primero, en la Universidad de Princeton y después, en la Universidad de Syracuse.

        De regreso en Inglaterra, Penrose dedicó los dos años siguientes 1961-63, como Asociado de Investigaciones en el King`s College, de Londres, antes de regresar nuevamente a los Estados Unidos, para estar el año 1963-64 como Profesor Asociado Visitante en la Universidad de Texas, en Austin. 

        En 1964, Penrose obtuvo el cargo como Lector en Birkbeck College, en Londres y dos años más tarde, fue promocionado como Profesor de Matemática Aplicada en este último. En 1973 le fue otorgada la posición como Profesor Rouse Ball de Matemática en la Universidad de Oxford y continuaría hasta que llegó a ser Profesor Emérito Rouse Ball de Matemática en 1998. En ese año, le otorgaron también la posición como Profesor Gresham de Geometría, en Gresham College, de Londres.

        A comienzos de 1959, Penrose publicó una serie de artículos importantes en Cosmología. El primero fue "La forma aparente de una esfera relativísticamente en movimiento"; mientras que en 1960 publicó "Un Espinor acercándose a la Relatividad General". Este último trabajo lo describió de esta manera:

Una detallada y elegante exposición... del aparato matemático de la teoría de la gravitación, que enfatíza la teoría geométrica de los tensores de Riemann...

        En 1965 usando métodos topológicos, Penrose probó un teorema importante, la cual bajo ciertas condiciones, mostró que una singularidad debe ocurrir en un colapso gravitacional. Básicamente, bajos estas condiciones, el espacio-tiempo no puede ser continuo y la relatividad general clásica falla. Penrose buscaba una teoría unificada, combinando la relatividad y la teoría cuántica, ya que los efectos cuánticos llegan a ser importantes en la singularidad.

"Roger revolucionó las herramientas en las matemáticas que usamos para analizar las propiedades del espacio-tiempo"

Kip Thorne.

Premio Nobel de Física por sus estudios sobre los Agujeros Negros, del Instituto Tecnológico de California-CALTECH.

        Uno de los más grandes logros de Penrose fue 1967, cuando inventó la Teoría de Twistores, que mapea objetos geométricos de un espacio de Minkowsky, en un espacio complejo de 4 dimensiones, con la signatura métrica (2,2). Esta es una teoría realmente importante, ya que combina poderosos métodos algebraicos y geométricos. Junto con Wolfgang Ridler, Penrose publico este primer volumen de Espinores y el Espacio-Tiempo en 1984 (detalles sobre esta teoría y otras de Penrose, mas adelante).

        En 1969, conjeturó la hipótesis de Censura Cósmica. Esta propone (de manera informal) que el universo nos protege de la inherente impredictibilidad de las singularidades (como los agujeros negros), ocultándolos de la vista. Esta forma es conocida actualmente como la Hipótesis Débil de la Censura Cósmica; en 1979, Penrose formuló una versión más firme, llamada la Hipótesis Fuerte de la Censura Cósmica. Esta nos dice que las singularidades siempre estarán, o bien enteramente en el futuro, como las singularidades de colapsos gravitatorio, o bien enteramente en el pasado, como el Big Bang.  En conjunción con la Conjetura BKL (Belinskii, Khalatnokov, Lifschitz) y problemas con la estabilidad no lineal, resolver la conjetura de la censura cósmica es uno de los problemas más importantes en la teoría de la relatividad.

La Conjetura BKL es un sistema de coordenadas donde el tiempo a la singularidad es la coordenada de tiempo. Estos asumen que los términos dominantes en las ecuaciones de campo son aquellas que involucran las derivativas de tiempo. 

        Penrose es conocido también por su descubrimiento en 1974, de los Teselados de Penrose, que están formados de dos teselas, que sólo pueden teselar el plano de forma aperiódica. En 1984, se encontraron patrones similares en la organización de átomos en Cuasicristales. Su contribución más importante puede ser su invención, en 1971, de las redes de espín, que posteriormente formó la geometría del espacio-tiempo en un bucle gravitónico cuántico. Penrose influyó en la popularización de los comúnmente conocidos como Diagramas de Penrose, conocidos también como Diagramas Causales.

        Es por un importante número de libros que Penrose es, tal vez, más conocido. Publicaría "La Nueva Mente del Emperador”: Concerniente a las computadoras, la mente y las Leyes de la Física" en 1989. El año siguiente, el libro fue premiado con el Premio Rhone-Poulenc de Ciencias. En 1994 Penrose publicaría "Sombras de la Mente: La búsqueda de la ciencia perdida de la Conciencia" el cual continuaba con el desarrollo del tópico aparecido en La Nueva Mente del Emperador.

        En 1996, Penrose publicaría junto con Stephen Hawking "La Naturaleza del Espacio-Tiempo". El libro posée un registro de un debate entre ambos científicos en el Instituto de Ciencias Matemáticas Isaac Newton, en la Universidad de Cambridge, en 1994. Cada uno de ellos ofreció tres lecturas en la que daban sus alternativas, por lo que cada uno respondería a los argumentos del otro, para que, en una sesión final, se genere un debate entre ambos. Aquí reseñamos la contribución de Penrose en la que claramente resalta su propia posición, y la de Hawking: 

"Al inicio de este debate, Stephen dijo que pensaba que el era un positivista, mientras que yo era un Platonista. Estoy feliz con el por ser un positivista, pero creo que el punto crucial aquí es que, más que esto, soy un realista. También, si uno compara este debate con el famoso debate entre Niels Bohr y Albert Einstein, hace unos 70 años, puedo pensar que ¡Stephen jugaba el rol de Bohr y yo el de Einstein! Para Einstein argumentar que puede existir algo como un mundo real, no necsariamente representada por una función de onda, mientras que Bohr argumentaba que la función de onda, no describe un micromundo "real" sino sólo un "conocimiento", que es necesario para hacer predicciones."

Penrose y la Mente.

        Lo que, posiblemente, ha dado más fama a Penrose, es su polémica teoría sobre la mente. Penrose ha argumentado que debe haber algo de naturaleza, no computable en las leyes físicas, que describen la actividad mental. Este argumento tiene como base el teorema de la Incompletitud de Gödel, que habla de la imposibilidad de una demostración formal de una cierta proposición matemática, aunque para el entendimiento humano ésta sea de hecho verdadera.

        Penrose como Hameroff, postulan que la mente y el cerebro son dos entidades separables. Hameroff, médico anestesista, lo hace a través de sus estudios sobre los microtúbulos y el citoesqueleto celular, especialmente en las neuronas, mientras que Penrose lo hace desde el teorema de la incompletitud.

Penrose, uno de los más grandes cosmólogos de la historia, dice que la mente y el Universo son regidos por teorías que aun no hemos descubierto.

        El modelo que defiende Penrose, junto con Hameroff, trata de explicar sucesos difíciles de entender a través de las neurociencias convencionales, y para ello se apoya en aspectos revisados de la teoría cuántica (por ejemplo, el concepto de coherencia), así como la existencia de un fenómeno físico, inédito hasta ahora, que parece darse en el interior de las neuronas, cuando la función de onda cuántica se colapsa por sí misma en una reducción objetiva orquestada.

"Estaba en el grupo de post-doctorado de Roger a mediados de los 70, en la que aprendi en grande durante esos dos años con Roger; incluso, mas que en cualquier periodo en mi subsecuente carrera academica. Esto, por supuesto, incluia mucho material tecnico en relatividad general y geometria. Sin embargo, aprendí algo más valioso, algo más intangible y profundo... observar a Roger seleccionando problemas científicos y llegando a soluciones con su única perspicacia geométrica, casi sin esfuerzo, con un toque de magia. Desde entonces, su manera de acercar la ciencia ha continuado teniendo una profunda influencia en todos mis trabajos."

Abhay Ashtekar.

Centro para Física Gravitacional y Geometría, Departamento de Física de la Universidad Estatal de Pennsilvania, Universidad Park, Estados Unidos.

        Penrose sugiere que ninguna máquina de computación podrá ser tan inteligente como un ser humano, ya que los sistemas formales algorítmicos (o sea, los sistemas de instrucciones secuenciadas sobre los cuales están construidas las computadoras) nunca les otorgarán la capacidad de comprender y encontrar verdades que los seres humanos poseen.

        Lo descrito hasta acá, es un "ápice" del aporte de Penrose a la ciencia. Sin embargo, es menester adentrarnos ahora en "aguas mucho más profundas" para resaltar la complejidad matemática a la que Penrose ha dedicado su muy larga y fructífera carrera, ampliando de forma más profunda, conceptos anteriormente descritos en términos más básicos.

La Pseudoinversa de Moore-Penrose.

        En matemáticas, y en particular álgebra lineal, la pseudoinversa A+ de una matriz A, es una generalización de la matriz inversa. El tipo de matriz pseudoinversa, más conocida es la llamada Pseudoinversa de Moore-Penrose, que fue descrita independientemente por E. H. Moore en 1920, Arne Bjerhammar en 1951, y Roger Penrose en 1955. Anteriormente, Fredholm introdujo el concepto de la pseudoinversa del operador integral en 1903. El término de la pseudoinversa de una matriz, generalmente se usa para referirse a la pseudoinversa de Moore–Penrose.

        Un uso común de la pseudoinversa es el de computar una solución de «ajuste óptimo» (por cuadrados mínimos) de un sistema de ecuaciones lineales que no posee solución única. Otro uso es hallar la solución de norma mínima (euclídea) de un sistema de ecuaciones lineales con múltiples soluciones. La pseudoinversa facilita el enunciado y la prueba de resultados del álgebra lineal.

La fórmula de cálculo de A+ es:

A = (At A) -1 At: donde AT es la transpuesta de A.

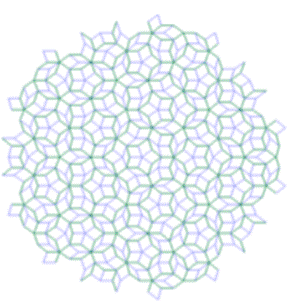
Teselación de Penrose.

        Una Teselación de Penrose o suelo de baldosas de Penrose, es una teselación no periódica generada por un conjunto aperiódico de baldosas prototipo, quien investigó dichos conjuntos en la década de los 70. Debido a que todas las teselaciones obtenidas con las baldosas de Penrose son no periódicas, las teselaciones de Penrose han sido consideradas como teselaciones aperiódicas. Entre el infinito número de posibles teselaciones hay dos que poseen eje de simetría y una simetría rotacional de orden cinco, como en el diagrama mostrado a la derecha, y el término de Teselación de Penrose usualmente se refiere a esos.

        La teselación de Penrose tiene varias propiedades a destacar:

1) Es no periódica, lo cual significa que carece desimetría translacional alguna. Dicho de manera simple, una copia desplazada nunca concordará con el original de forma exacta.

2) Cualquier región finita en una teselación aparece un número infinito de veces en esa teselación y de hecho, en cualquier otra teselación. Esta propiedad podría ser trivialmente verdadera en una teselación con simetría translacional, pero es no trivial cuando se aplica en las teselaciones no periódicas de Penrose.

3) Es un Cuasicristal: implementada como una estructura física, una teselación de Penrose producirá una difracción de Bragg cuyo patrón de difracción revela la simetría subyacente de orden cinco y el orden en un margen amplio. Este orden refleja el factor por el cual la teselación está organizada, no a través de simetría rotacional, pero sí a través de un proceso, algunas veces llamado, “deflación” o “inflación”.

Una teselación de Penrose.

        La teselación de Penrose original fue propuesta en 1974 en un documento titulado el "Papel de la estética en la investigación pura y aplicada". No más de una quinta parte del documento trata de ello, pero Penrose admite que la teselación fue el tema real. Más tarde, Penrose reconoce la inspiración del trabajo de Johannes Kepler. En su libro "Harmonices Mundi Kepler" exploró teselaciones construidas por medio de pentágonos y se demostró que su construcción podía ser extendida en una teselación de Penrose. En un principio los trazos de esta idea ya estaban hechos en un trabajo de Durero.

        Al intentar llenar de baldosas el plano con pentágonos regulares es necesario dejar huecos. Penrose encontró una particular forma de teselado en el cual los huecos podían ser llenados con otras formas: una estrella, un bote y un diamante como se muestra a la izquierda. En adición a las baldosas, las reglas de comienzo de Penrose, usualmente llamadas reglas de ensamble, especifican como las baldosas deben ser unidas entre sí; estas reglas son necesarias para asegurarse de que las teselaciones sean no periódicas.

Una teselación construida del conjunto original de Penrose (P1) de seis baldosas.

        Como hay tres conjuntos distintos de reglas de ensamble para baldosas pentagonales, es común considerar al conjunto como si tuviera tres baldosas pentagonales diferentes, mostradas con colores diferentes en la ilustración. Esto resulta en un conjunto de seis baldosas: un rombo delgado o "diamante", una estrella de cinco picos, un "bote" (aproximadamente 3/5 de una estrella) y tres pentágonos.

La teselación de Penrose Pentagonal (P1) en negro, sobre una teselación rómbica coloreada de fondo (P3).

        Penrose encontró más tarde dos conjuntos más de baldosas aperiódicas, uno consistiendo en baldosas conocidas como "cometa" y "flecha" (P2) y un segundo conjunto consistiendo en dos rombos (P3). La traslación entre la teselación P1 y su correspondiente teselación P3 es mostrada arriba.

        En lo referente a los rombos de Penrose, son un par de rombos de lados iguales pero de formas diferentes.

1) El rombo más delgado t tiene cuatro esquinas con ángulos de 36, 144, 36 y 144 grados. El rombo t podría ser bisectado a lo largo de su diagonal menor para formar un par de triángulos de Robinson.

2) El rombo grueso T tiene ángulos de 72, 108, 72 y 108 grados. El rombo T podría ser bisectado a lo largo de su diagonal mayor para formar un par de triángulos de Robinson obtusos.

        Hay 54 combinaciones ordenadas cíclicamente que suman hasta 360º en un solo vértice, pero las reglas de las teselación solo permiten que aparezcan 7 de esas combinaciones. Las baldosas ordinarias en forma de rombo pueden ser usadas para llenar el plano de forma periódica, por lo que hay restricciones que deben de hacerse sobre como las baldosas pueden ser ensambladas. La regla más simple, prohíbe que dos baldosas de la misma naturaleza sean colocadas juntas para formar un paralelogramo simple, esto es suficiente para asegurar la aperiodicidad.

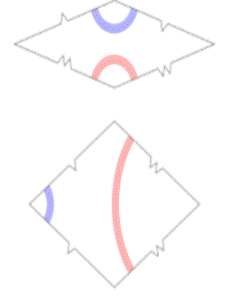
Dos tipos de regla de ensamble para los Rombos de Penrose.

        Aun así, las reglas están hechas para distinguir los lados de las baldosas y requerir que solo lados particulares puedan ser colocados juntos entre las baldosas. Un ejemplo de reglas para encajar de forma adecuada es mostrada en la parte de arriba en el diagrama de la izquierda. Las baldosas deben ser ensambladas de manera que las curvas que cruzan sus bordes concuerden en color y posición. Una condición equivalente es que las baldosas deben ser ensambladas de tal manera que las muescas de sus bordes encajen juntos. Las mismas reglas pueden ser establecidas para otras formulaciones.

        Hay una gran cantidad de patrones finitos arbitrarios con simetría de grado diez y que cuando mucho tienen un punto de centro de simetría de grado diez global donde diez ejes de simetría lo cruzan. Como la teselación es aperiódica, no hay simetría translacional, el patrón no puede ser desplazado para que coincida consigo mismo en el plano entero.

Penrose sonríe, mostrando orgullosamente su creación de las Teselaciones.

        Sin embargo, cualquier región delimitada, no importa cuán grande, será repetido un número infinito de veces dentro de la teselación. Por eso un finito número de patrones no pueden ser diferenciados entre las incontables teselaciones de Penrose, ni siquiera para determinar en que posición se está dentro de la baldosa que está siendo mostrada. La única manera de distinguir las dos teselaciones simétricas de Penrose de las otras es que su simetría continúe al infinito.

        Los rombos pueden ser cortados a la mitad para formar un par de triángulos, llamados los triángulos de Robinson, los cuales pueden ser usados para producir las teselaciones de Penrose con una sustitución de baldosas. Los triángulos de Robinson son los triángulos isósceles 36º-36º-108º y 72º-72º-36º. Cada uno de estos triángulos tienen los bordes en la relación de (1+√5):2, la razón dorada. Las reglas que hacen cumplir la aperiodicidad en una teselación de triángulos de Robinson hacen a los triángulos asimétricos, y cada triángulo aparece en conjunción con sus reflejos para formar un rombo, una cometa o una flecha.

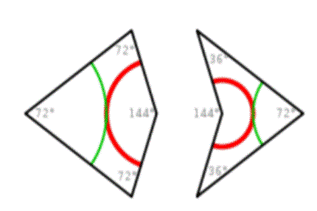
Las baldosas de la Cometa y la Flecha.

        Los cuadriláteros llamados la "cometa" y la "flecha" también son usados para formar una teselación de Penrose.

1) La cometa es un cuadrilátero cuyas cuatro esquinas tienen ángulos de 72, 72, 72 y 144 grados. La cometa puede ser bisectado a lo largo de su eje de simetría para formar un par de triángulos acutángulos de Robinson.

2) La flecha es un cuadrilátero no convexo (cóncavo) que tiene cuatro ángulos interiores que son de 36, 72, 36 y 216 grados. La flecha puede ser bisectada a lo largo de su eje de simetría para formar un par de triángulos obtusángulos de Róbinson.

        Los arcos verde y rojo en la baldosa limitan el posicionamiento de las baldosas: cuando dos baldosas comparten un borde en una teselación, los patrones deben concordar con estos bordes. Por ejemplo, el vértice cóncavo de una flecha no puede ser llenado simplemente con una cometa, pero puede ser llenado con un par de cometas.

Baldosas de Penrose que adornan el piso del edificio MCS de la Universidad de Western, Australia.

        Pentaplex Ltd, una compañía de Yorkshire, Inglaterra manejada por Penrose, es la titular de los derechos de las teselaciones. Penrose y Pentaplex presentaron una demanda contra Kimberly-Clark. Esta había, supuestamente, hecho en relieve las teselaciones de Penrose en las texturas de papel de baño marca Kleenex en Reino Unido. La empresa de productos para higiene SCA, llegó después a controlar los productos Kleenez y alcanzaron un acuerdo con Penrose y Pentaplex, en la demanda en cuestión de la teselación de Penrose. SCA no está involucrada en la disputa de copyright.

La Secuencia de Fibonnaci y el Radio Dorado.

        La teselación de Penrose, la Secuencia de Fibonacci y el Radio Dorado están intrínsecamente relacionadas y tal vez, deberían ser considerados como aspectos diferentes del mismo fenómeno.

1) La relación de los rombos gruesos con los delgados en un teselado infinito es la razón dorada T/t = φ = 1.618...

2) Alrededor de cada estrella 5T- se forma una espiral de Fibonnacci segmentada por los lados de los rombos.

3) La distancia entre los montículos finitos repetidos en la teselación, crece con los números de Fibonacci, cuando el tamaño del montículo se incrementa.

4) Los eigenvalores de la matriz de substitución son φ+1 (=φ²) y 2-φ (=1/φ²).

5) La distribución de frecuencias de oscilación en una teselación de Penrose muestra las bandas y huecos cuyos anchos están en proporción expresada por φ.

6) El esquema de sustitución T - 2T+t;t - T - + t introduce φ como un factor de escala, su matriz es la raíz de la matriz de substitución de Fibonnacci, implementada como una secuencia de símbolos (ejemplo, 1→101, 0→10) esta substitución produce una serie de palabras cuyas longitudes son los números de Fibonnacci con índice inusual, F(2n+1) para n=1,2,3.., el límite se vuelve la secuencia Binaria Infinita de Fibonacci.

En la búsqueda del Radio Dorado.

La búsqueda del Radio Dorado, como una proporción geométrica, descubierta en la antigüedad, se relaciona a diversos aspectos como la escultura, botánica, orbitas de los planetas y en la termodinámica de los agujeros negros. El deja vu no es un término generalmente aplicado a las matemáticas; sin embargo, ciertos números tales como ángulos, radios, constantes, tiene una manera de perseguir ciertas regularidades.

Muchos están familiarizados con el número pi (3,1415...). Este símbolo numérico derivado del radio del diámetro de un círculo a su circunferencia, la cual reaparece a través de la geometría y la física. Esta letra griega no está sola: un segundo símbolo, φ (phi), llega para reclamar su presencia en las matemáticas y la ciencia.

El Radio Dorado da forma al mundo alrededor de nosotros. El hecho de que este número se muestra repetidamente a través de la naturaleza, fue reconocido en la antigüedad, cuando Euclides de Alejandría se topo con su significado. Generaciones de sucesores se advocaron a develar el misterio del Universo y descubrir su significado, desde Ptolomeo y Johannes Kepler, y los matemáticos Luca Pacioli y Martin Ohm.

La historia del radio dorado comenzó con Ptolomeo I, sucesor de Alejandro el Grande. Entre sus primeros grandes actos fue establecer una escuela conocida como "Museo" en Alejandría, Egipto. Fundada alrededor del año 300 B.C. esta antigua universidad, incluía entre sus profesores, al padre de la geometría deductiva formal: Euclides.

"Estoy seguro que, para todos nosotros, Penrose resalta entre las personas que han pensado más profundamente y más ingeniosamente sobre la naturaleza del espacio-tiempo".

Graeme Segal.

Departamento de Matemática Pura y Estadística Matemática, Universidad de Cambridge, 16 Mill Lane, Cambridge, Inglaterra.

Euclides produjo el libro Elementos, donde definió la geometría y la teoría de los números. Descubrió el radio dorado después de buscar la relación entre segmentos lineales. Platón, vio en la naturaleza, en términos perfectos, e idealizo formulas matemáticas. Para él, la simetría era suprema, y propuso los famosos cuatro elementos  del universo: tierra, agua, aire y fuego; por su parte, Johannes Kepler, grandemente admiro el radio dorado, creyendo que este era una parte fundamental de Dios y su plan para el cosmos. En sus propias palabras: "Creo que esta proporción geométrica sirve como idea para el Creador".

Penrose y la Edad Dorada de la Astronomía.

Siguiendo los pasos de Kepler y el grupo de pensadores de la antigüedad, la historia del radio dorado y la Cosmología, tuvieron que esperar cerca de cuatro siglos para abrir un nuevo capítulo. Para ello, el físico Paul Steinhardt, Profesor de la Cátedra Albert Einstein, de la Universidad de Princeton, Estados Unidos, y el Cosmólogo Roger Penrose, de la Universidad de Oxford, Inglaterra, revivieron esta historia numérica.  

Ambos científicos, además de ser reconocidos por sus importantes investigaciones en Cosmología, también son unos consumados matemáticos. Mientras Steinhardt es una figura clave en el desarrollo de los actuales modelos inflacionarios del universo, Penrose investiga las teorías de Einstein en los casos más extremos de la formación de los agujeros negros; también fue el primero en reconocer una discontinuidad científica entre la mecánica cuántica y la relatividad.

Más allá de sus exploraciones teóricas del distante Universo, estos cosmólogos se sintieron atraídos por el radio dorado y su más terrenal aparición en el campo de los cuasícristales. La mayoría de los sólidos son, o amorfos o cristalinos en la naturaleza. Examinadas bajo los más altos niveles de magnificación, los materiales amorfos, tales como el vidrio, parecen estar hechos de átomos que están unidas sin ninguna estructura ordenada.

Las estructuras cristalinas, tales como la Sal, forman células unidas de grupos de átomos con una estructura repetida. Tal como un piso de mosaico, la orientación de cada unidad de célula determina el patrón entero. Por muchas décadas, los científicos han conocido que formas con simetría de cuatro lados (cuadrados) simetría de tres (triángulos), y de seis (hexágonos) pueden llenar el plano de una superficie, usadas por la naturaleza para formar cristales. Al mismo tiempo, los científicos creían que cristales con simetría de cinco lados no existían.

En 1984, un equipo de investigadores liderizados por el ingeniero en materiales israelí, Dany Schectman, descubrió que los cristales de una aleación de aluminio manganeso, exhibía una simetría quíntuple. Esto significaba, que su estructura aparecía igual cuando el cristal es visto después de ser rotado un quinto de un circulo, o 360 grados ÷ 5 - 72 grados. Este descubrimiento impactó a los cristalógrafos. Los cristales de Schectman demostraron que otro estado de la materia, denominada "Cuasícristales", existe, y comparte aspectos tanto, con las sustancias amorfas y cristalinas.

No le tomo mucho tiempo a los físicos mostrar que por un descubrimiento hecho en 1974 en matemática recreacional por Penrose, les dio luz en el misterio de los cuasicristales. Penrose se sintió fascinado con descubrir un set de formas no periódicas que podían ser usadas para llenar un plano o enlosar un piso. Después de años de búsqueda, Penrose encontró dos formas básicas de baldosas llamadas "Flechas" y "Cometas" que pueden unirse, para llenar un plano. Flechas y Cometas exhiben la simetría "prohibida" de cinco, y son derivadas de diferentes combinaciones del triángulo dorado de Ptolomeo.

De forma extraordinaria, fue el trabajo de dos cosmólogos (Penrose y Steindardt) interesados en las escalas más grandes imaginables, quienes determinaron la naturaleza de las minúsculas formaciones atómicas. El nexo entre el radio dorado y la astronomía no finaliza aquí. En adición a su presencia dentro del mundo atómico, el radio dorado se esconde allá arriba, en el Universo.

Los sistemas auto-gravitatorios como las estrellas, tienen la propiedad de calentarse cuando pierden energía. Los Agujeros Negros que no poseen rotación (Agujeros Negros de Schwarzschild) tienen la misma forma; agujeros negros giratorios (Agujeros Negros de Kerr), pueden experimentar una interesante fase de transición en el cual, se transforman de un estado con calor negativo específico, a un estado de calor positivo específico. Sorprendentemente, el físico Paul Davies, mostró que esta transición ocurre cuando el radio del cuadrado de la masa del agujero negro, al cuadrado de su momento angular (en unidades apropiadas), iguala el radio dorado.

Luego de haber repasado ciertos aspectos relacionados a la profunda matemática desarrollada por Penrose, tales como las teselaciones, pseudoinversa, radio dorado, nos sumergiremos en el campo de la Cosmología y el papel de Penrose en su desarrollo.

Cosmología Cíclica Conforme.

La Cosmología Cíclica Conforme o Teoria de los Eones es un modelo cosmológico en el marco de la relatividad general, defendido por los físicos teóricos Roger Penrose y Vahe Gurzadyan. En la CCC, el universo se repite a través de ciclos infinitos, en los cuales el infinito de tipo tiempo de cada iteración anterior, se identifica con la singularidad del Big Bang del siguiente. Penrose popularizó esta teoría en su libro Ciclos del tiempo: Una extraordinaria nueva visión del universo, publicado en lengua inglesa en 2010.

La idea básica de Penrose es conectar una secuencia numerable de espacio-tiempos abiertos según el modelo FLRW (Friedman, Lemaître, Robertson, Walker) cada uno implicando un Big Bang seguido de una expansión infinita en el futuro. Penrose advierte que el límite pasado de conformación de una copia de un espacio-tiempo FLRW puede ser "conectado" con el límite futuro de conformación de otro, después de un tránsito de tipo "transformación conforme".

En particular, cada medida FLRW individual se multiplica por el cuadrado del factor conforme, que se aproxima a cero en un infinito de tipo tiempo, de alguna "aplastando"  forma el límite futuro de formación en una hipersuperficie conforme regular (que sería de tipo espacio, de existir en efecto una constante cosmológica positiva, como actualmente se cree).

El resultado es una nueva solución de las ecuaciones de Einstein, que Penrose aplica a escala universal y que se compone de una secuencia de ciclos o sectores que este científico denomina "eones".

En su libro, Ciclos del tiempo, Penrose explica la transición entre eones, aun definidos por fronteras de magnitudes extremas, de la siguiente forma:

"Quizás, el lector se sienta preocupado por la identificación de un futuro remoto, donde la radiación se enfría hasta temperatura cero y se expande hasta densidad cero, con una explosión de tipo big bang, donde la radiación ha empezado a una temperatura infinita y una densidad infinita. Pero el "estiramiento" conforme en el big bang reduce esta temperatura y esta densidad infinitas a valores finitos, y la "compresión" conforme en el infinito aumenta la densidad y la temperatura nulas a valores finitos. Estos son precisamente los tipos de reescalado que hacen posible que los dos encajen, y el estiramiento y la compresión son procedimientos a los que la física relevante en uno u otro lado es completamente insensible. También puede mencionarse que el espacio de fases P, que describe la totalidad de los estados posibles de toda la actividad física en uno u otro lado del tránsito […], tiene una medida de volumen que es conformemente invariante, básicamente por la razón de que cuando las medidas de distancia se reducen, las correspondientes medidas de momento aumentan (y viceversa) de tal manera que el producto de las dos, no es en absoluto, afectado por el reescalado (un hecho que será de importancia crucial para nosotros […]). Llamo a este esquema cosmológico, Cosmología Cíclica Conforme, abreviada como CCC".

         La característica más importante de este modelo para la física de partículas es que, dado que los bosones obedecen las leyes de la teoría conforme de campos, se comportarán de la misma manera en los eones reescalados que en sus contrapuntos FLRW originales. (Clásicamente, esto se corresponde con el hecho de que la estructura del cono de luz se conserva en una reestructuración conforme.)

        Para este tipo de partículas, el límite entre eones no es un límite en absoluto, sino simplemente una superficie de tipo espacio que puede atravesarse como cualquier otra. Los fermiones, por otro lado, permanecen confinados en un eón dado. Esto proporciona una solución conveniente a la paradoja de la información de los agujeros negros; de acuerdo con Penrose, los fermiones se convierten irreversiblemente en radiación en el proceso de evaporación de un agujero negro, de forma que se preserve la suavidad en la frontera entre eones.

        Las propiedades de curvatura de la cosmología de Penrose son verosímiles. En primer lugar, el límite entre eones satisface la hipótesis de la llamada Curvatura de Weyl, proporcionando así un cierto tipo de pasado de baja entropía, como es el requerido por la mecánica estadística y por la mera observación. En segundo lugar, Penrose ha calculado que una cierta cantidad de radiación gravitacional se preserva a través del límite entre eones. Penrose sugiere que esta radiación gravitatoria extra puede ser suficiente para explicar la aceleración cósmica observada, sin necesidad de apelar a un campo material de energía oscura.

        En 2010, Penrose y Vahe Gurzadyan publicaron un avance de estudio en el que afirmaban que las observaciones del fondo cósmico de microondas, realizadas por el satélite Wilkinson Microwave Anisotropy Probe y el Experimento BOOMERanG, mostraron anomalías concéntricas que eran consistentes con la hipótesis de la CCC, sugiriendo una baja probabilidad de que esas observaciones fueran resultado de la casualidad.

        Dichas observaciones podrían manifestar que la llamada radiación de fondo de microondas, o radiación del fondo cósmico, registra ecos de eventos similares al Big Bang ocurridos con anterioridad al mismo. Estos ecos aparecen como "anillos" concéntricos alrededor de grupos de galaxias, en los cuales, la variación en el fondo cósmico es inusualmente baja.

        El profesor Shaun Cole, de la Universidad de Durham, Inglaterra, declaró en su día a la BBC, sobre la investigación de Penrose y Gurzadyan:

«Es admirable [...]. Es una teoría revolucionaria, y ahora parece haber datos que la apoyan. [...] En el modelo estándar del Big Bang no hay nada cíclico, tiene un comienzo y no tiene un fin. [...] La pregunta filosófica que es pertinente plantear es ¿qué ocurrió antes del Big Bang?, y lo que intenta esta teoría es eliminar la respuesta de "no hubo nada antes" y convertirlo en un evento cíclico».

        Cole expresó, sin embargo, cierta sorpresa ante la pretensión de que la variación estadística en los datos de la radiación de microondas sea la rúbrica más obvia de lo que puede convertirse en una idea revolucionaria. «Hay otras cosas que podrían haber ocurrido en la última parte del último eón. ¿Por qué no muestran indicios mayores?», se preguntó este científico.

        De hecho, la significación estadística precisa de las observaciones aludidas ha sido cuestionada desde entonces. Tres grupos de trabajo han intentado independientemente reproducir estos resultados, pero se encontró que la detección de las anomalías concéntricas no era estadísticamente significativa, en el sentido de que tales círculos aparecerían en una simulación gaussiana de la anisotropía en los datos sobre la CMB.

        La razón del desacuerdo se enfocó a la cuestión de cómo diseñar las simulaciones que se utilizan para determinar significados: los tres intentos independientes para repetir el análisis de todas las simulaciones utilizadas se basan en el modelo Lambda-CDM estándar, mientras que Penrose y Gurzadyan, utilizan un enfoque no estándar aún no verificado.

        En 2013, Gurzadyan y Penrose publicaron un estudio de mayor alcance, y también, presentaron un nuevo método, denominado the sky-twist transformation (algo así como "transformación de torsión celeste"), que no se basa en simulaciones.

Diagrama Penrose-Carter.

        En física teórica, al tratar de representar pictóricamente un espacio-tiempo surgen dos problemas:

1) El espacio-tiempo es una variedad de dimensión 4. Podemos obviar esto usando las simetrías del mismo, en caso de tenerlas, y representar una subvariedad de dimensión 2. Por ejemplo, para un espacio-tiempo esféricamente simétrico, todos los puntos de una 2-esfera son equivalentes, y se pueden representar por un solo punto de un diagrama.

2) Las coordenadas del mismo se extienden hasta infinito. Esto puede solventarse sustituyendo el espaciotiempo físico por un espacio-tiempo no físico conforme con el primero.

Diagrama de Penrose de un Espacio-Tiempo Minkowski Infinito. Elimina dos dimensiones espaciales y concentra en una región infinita (en este caso, con forma de diamante) el resto, mediante el efecto de transformación conforme.

        Ambos problemas quedan solventados con los diagramas conocidos como diagramas conformes, diagramas de Penrose-Carter o simplemente Diagramas de Penrose, diagramas bidimensionales que conservan la información sobre las relaciones causales entre diversos puntos del espacio-tiempo y permiten representar regiones infinitas en diagramas finitos. Para ello, sacrifican información sobre las distancias entre puntos.

        La métrica de los diagramas de Penrose-Carter es conformemente equivalente con una restricción bidimensional de la métrica real del espacio-tiempo que representan. El factor conforme es elegido de modo, que todo el espacio-tiempo se proyecte en un diagrama de dimensiones finitas. La frontera de la nueva figura no formará parte del espacio-tiempo original, pero permitirá estudiar sus propiedades asintóticas y sus singularidades.

        Penrose lo uso por vez primera en 1962, junto a su colega Brandon Carter, que los sistematizó en 1966. Un diagrama de Penrose-Carter comparte varias características con el espacio-tiempo de Minkowsky: las líneas oblicuas a 45° corresponden a trayectorias luminosas, la dimensión vertical representa una coordenada temporal y la horizontal a las dimensiones espaciales.

Espacio de Minkowsky.

        Para representar el diagrama conforme de un espacio de Minkowsky, podemos pensar en la expresión de su métrica plana en coordenadas esféricas, y restringirnos a la subvariedad cubierta por las coordenadas r y t. Estas coordenadas abarcan un rango infinito. Un primer intento de conseguir que cubran un rango finito sería usar las nuevas coordenadas T = arctgt y r = arctgr  Pero esto no conseguiría mantener los conos de luz de nuestro diagrama a 45º. Para conseguirlo, se realiza un triple cambio de coordenadas:

- En primer lugar, el cambio a las coordenadas nulas u = t - r, v = t + r.

- Sobre ellas, efectuamos el cambio U = arctan u, V = arctan u

- Finalmente, volvemos a coordenadas T = U + V, R = V. U

La métrica en estas coordenadas queda expresada por:

Donde: w = cosT + cos R

Espacio de Schwarzschild.

        La figura muestra la representación de un Espacio de Schwarzschild, correspondiente a un agujero negro estático (sin rotación). La coordenada vertical llamada "u" es la temporal, mientras que la coordenada horizontal "v" es espacial. El diagrama de Penrose es conforme, es decir, que las geodésicas de género nulo (líneas de luz) corresponden a la media-primero y segunda bisectrices "altas".

De este sistema de coordenadas, derivado del de Kruskal, se tiene:

El diagrama hecho entonces por abstracción de dos coordenadas esféricas θ y φ  Los conos de luz delimitados por las geodésicas nulas (ds² = 0) correspondiente a du² = dv², entonces {u = v} ou {u = -v}, es decir, las bisectrices primera y segunda

Diagrama de Penrose de un Espacio-Tiempo de Schwarzschild. El eje horizontal representa la coordenada espacial v, y el vertical la coordenada temporal u (no deben confundirse con las coordenadas nulas del espacio de Minkowsky).

        Partiendo de la izquierda, dos rectas (primera y segunda bisectrices) divergen: la recta de abajo, llamada I-, representa "lo infinito del pasado", de ésta provienen todos los móviles desde lo infinitamente lejano; la recta de arriba, I+, corresponde al "infinito del futuro", y representa el lugar hacia donde se dirigen todos los móviles que se distancia luego de un agujero negro.

        Las dos rectas horizontales y paralelas, representan la singularidad (en el pasaje del pasado al futuro), situado en r = 0. Este diagrama es simétrico por relación con la vertical. En línea discontinua está representado el horizonte de un agujero negro ubicado (en unidades convencionales) en r = 2M.

Los Twistores de Penrose.

         La Teoría de Twistores es una teoría matemática propuesta inicialmente por Penrose en 1967, que mapea los objetos geométricos del espacio-tiempo tetradimensional (Espacio de Minkowsky) en objetos geométricos del espacio complejo tetradimensional con signatura métrica (2, 2). Las coordenadas en tal espacio se denominan twistores. La teoría de twistores resulta especialmente adecuada para solucionar las ecuaciones del movimiento de los campos sin masa de espín arbitrario.

Un rayo de luz (fotón) representado como un Twistor, de acuerdo a la Teoría de Penrose.

        En vez de tratar de explicar cómo las partículas se mueven e interactúan dentro del espacio y del tiempo, la teoría de los twistores propone que el espacio y el tiempo son construcciones secundarias que emergen desde un nivel más profundo de la realidad. En gravedad cuántica, se considera habitualmente que la geometría del espacio-tiempo debe fluctuar a escalas cuánticas, alterando cómo los eventos se relacionan entre sí.

        Debido a estas fluctuaciones cuánticas del espacio-tiempo, un evento que se supone es la causa de otro, puede no serlo rompiendo la noción de tiempo real y de causalidad, creando paradojas como las encontradas en las historias de viajes en el tiempo. En la teoría de los twistores, por el contrario, las secuencias causales son primarias, y no fluctúan. En cambio, el lugar y la duración de los eventos si lo hacen.

        Los twistores son una generalización de una teoría anterior, la de los espinores de Paul Dirac, donde se describía el espín de las partículas a la luz de la teoría de la relatividad y la mecánica cuántica. Los twistores son estructuras matemáticas que definen el movimiento y el espín de las partículas y constituyen los "puntos" de un espacio de cuatro dimensiones complejas (ocho dimensiones "reales").

        En una analogía, un twistor se puede representar como una familia retorcida de círculos, situada en un sistema de rosquillas encajadas unas dentro de otra. El propio sistema así construido se desplazaría en su totalidad a la velocidad de la luz.

        En la teoría de los twistores, el concepto de espacio-tiempo se desvanece como consecuencia del principio de incertidumbre, dando regiones difusas. Los twistores individuales representan partículas sin masa, es decir, los Bosones. Las partículas con masa o Fermiones, quedan determinadas por dos o más twistores. Dos de ellos describen los electrones y el resto de Leptones. Tres, los protones, neutrones y otros hadrones.

Penrose, tras el pizarrón, aparece junto a su creación: el posible camino descrito por un fotón de luz, en forma de un Twistor.

        Las partículas exóticas como, por ejemplo, algunos Quarks, están modelados por más de tres twistores. Las fuerzas se contemplan como deformaciones del espacio twistor. Los bosones distorsionarían el espacio-tiempo porque son portadores ellos mismos de distorsiones, esto es, los propios twistores.

"Soy un gran admirador de Roger, pero no pretendo conocerlo a el tan bien como la mayoria de ustedes. Dejenme, sin embargo, hablarles de un pequeño episodio de mi vida, indirectamente relacionada con el. Hace un par de años adquiri "La Nueva Mente del Emperador", justo antes de dejar mis vacaciones en el sur de Francia. Lleve el libro conmigo, esperando, por supuesto, disfrutar mis vacaciones, tanto así, que "olvide" el libro en mi maletín. Las cosas marcharon de forma diferente: en mi primera leccion de tenis, fui afectado por un lumbago y terminé mis vacaciones leyendo el libro una y otra vez en la piscina del hotel... otra mañana, fui a una libreria local y compre "Sombras de la Mente". Luego, estuve planeando tomar otras vacaciones en Italia en un par de semanas, y de repente, comenze a sentir un extraño dolor en mi hombro izquierdo. No soy supersticioso, pero..."

 Gabriele Veneziano.

División Teórica, CERN, Ginebra, Suiza.

        Los twistores tienen una curvatura de tipo helicoidal que describe la quiralidad de las partículas, las vulneraciones de la paridad en interacciones débiles, tal vez la distinción entre carga positiva y carga negativa y, posiblemente también, el sentido único del tiempo. La teoría de twistor surgió con el convencimiento de que la ausencia de antimateria no era exclusivamente una consecuencia de la ruptura de la simetría (ver ruptura espontánea de simetría) como se sugirió en las TGU (Teoría de Gran Unificación) y en sus ideas sobre las simetrías CPT. (la simetría C significa que las leyes son las mismas para partículas y antipartículas; la simetría P implica que las leyes son las mismas para una situación cualquiera y para su imagen especular: la imagen especular de una partícula girando hacia la izquierda y la simetría T que postula que si se invirtiera la dirección del movimiento de todas las partículas y antipartículas, el sistema volveria a ser igual a como fue antes: en otras palabras, las leyes son las mismas en las direcciones hacia adelante y hacia atrás en el tiempo) .

        La teoría de twistor es asimétrica respecto de la carga, la quiralidad y el tiempo, por lo que parece estar de acuerdo a la aparente vulneración de la simetría CPT en gravedad y cosmología cuántica. De hecho, atendiendo a las ecuaciones de esta teoría, el sentido del tiempo no es algo que haya adquirido el Universo después del Big Bang. Apareció en la estructura esencial del vacío primigenio.

Penrose recibiendo un de los tantos reconocimientos que acumula a lo largo de su carrera. Aquí aparece recibiendo el Doctor Honoris Causa, del Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional.

        Durante muchos años después de la publicación de Penrose en 1967, la teoría de twistor progresaba muy lentamente, en parte debido a problemas matemáticos. La teoría de twistor tampoco parecía relacionada con las ideas de la física contemporánea. Mientras que la teoría de twistor parecía decir algo sobre la gravedad cuántica, sus posibles contribuciones para la comprensión de las otras fuerzas fundamentales y de la física de partículas eran menos evidentes.

"Tal vez, el más importante y más robusto resultado del estudio de acercamientos no-perturbativos a la gravedad cuántica, es que el estado de los espacios de un gran set de teorías, puede ser descrito en términos de redes de espín, las cuales fueron inventadas por Roger Penrose a comienzos de los 60. En su contribución, es un honor para Roger que cuente la historia de cómo es que su redes de espín, inventadas originalmente como un modelo simple para la geometría cuántica discreta, ha llegado a ocupar un lugar central en gravedad cuántica".

Lee Smolin.

Centro para Física Gravitacional y Geometría, Departamento de Física de la Universidad Estatal de Pennsilvania, Estados Unidos.

        La teoría de twistores no logró precisar en qué consiste las fluctuaciones del lugar y la duración de los eventos, hasta que los teóricos de cuerdas mostraron que un evento de localización y tiempo ambiguos era en realidad una cuerda. La teoría de cuerdas tenía una prometedora explicación para la creación de un espacio, pero no podían hacerla funcionar. Se conjeturó que las partículas moviéndose en cuatro dimensiones pueden comportarse simplemente como cuerdas interaccionando en cinco dimensiones.

        Lamentablemente este mecanismo sólo producía una dimensión espacial altamente curvada. Usando twistores, se consiguió demostrar cómo todas las  dimensiones del espacio ordinario, incluido el tiempo, pueden aparecer.

         Edward Witten, del Instituto de Estudios Avanzados de la Universidad de Princeton, New Jersey, Estados Unidos, fue quién propuso la conexión entre la teoría de cuerdas y la geometría twistor, llamando a esta unificación "Teoría de Cuerdas Twistor". Desarrolló la manera de hacer teoría de cuerdas en un espacio twistor, cuya dimensionalidad era necesariamente la misma que la del espacio-tiempo 3 +1 de Minkowsky.

Nacido en un entorno familiar de destacados profesionales, Roger Penrose, con su personalidad cabal y calidad humana, se labró su propio futuro, sin apego al éxito de su familia. Dentro de la comunidad científica, es una personalidad respetada y admirada.

        La teoría de cuerdas twistor es, por tanto, una posible manera de eliminar la necesidad de más de tres dimensiones espaciales, cuando se trabaja con una teoría de (super)cuerdas. Aunque Witten afirmó que creía que la teoría de cuerdas twistor era algo que sólo funcionaba en parte, su trabajo ha dado nueva vida al programa de investigación twistor. Por ejemplo, la teoría de cuerdas twistor puede simplificar el cálculo de la dispersión de amplitudes de los diagramas de Feynman.

Teorema de las Singularidades de Penrose.

Hablar sobre las singularidades, es posiblemente, y de acuerdo con el redactor de la presente biografía (aunque me parece más una tesis) la epitome en la dilatada carrera de Penrose, por sus implicaciones científicas y el papel que esta tiene en los ámbitos de la relatividad y la mecánica cuántica. El teorema de las singularidades representa el primer resultado genuino post-Einsteniano en Relatividad General, en la que los conceptos fundamentales de una superficie atrapada fueron introducidos. 1965 fue ese año en la historia de la relatividad general. El descubrimiento e interpretación de la Radiación de Fondo Cósmico, junto con el teorema de la singularidad fueron publicados; a pesar de que ambos descubrimientos sucedieron en 1964, un año, no solo rígido para la mitad de esa década, sino también, exactamente 50 años después del nacimiento de la ecuación de campo de Einstein:  

El impacto y legado del teorema de la singularidad de Penrose representa una contribución clave para el renacimiento de la teoría. El muy aclamado teorema de la singularidad es reconocido por muchos como uno de los más grandes hechos en Relatividad General, Geometría Lorentziana y Física Matemática. A pesar de que existen varios resultados previos sobre singularidades, el teorema de Penrose es, sin lugar a dudas, el primero de los teoremas por su forma moderna, conteniendo nuevos e importantes ingredientes, fructíferas ideas que inmediatamente, llevaron a muchos y nuevos desarrollos en relatividad teórica, y por las devastantes consecuencias físicas concernientes al origen del Universo y el colapso de las estrellas masivas.  

Fue Penrose que, a partir de 1965, con su Teorema de las Singularidades, le dio presencia a la Teoría de la Relatividad de Einstein.

En particular, Penrose introdujo la incompletitud geodésica para caracterizar las singularidades; uso la noción de una hipersuperficie Cauchy (y por ende, de la hiperbolicidad global) y más importante, presento a la comunidad gravitacional con un regalo precioso en la forma de un novel concepto: superficies cerradas y atrapadas. A partir de 1965, la Relatividad General dejó su adolescencia detrás, emancipado de su creador, para convertirse en una teoría completamente madura, llena de vitalidad y sorpresas.

Antes de 1965 existían muchas indicaciones de que algún tipo de irregularidades catastróficas, digamos "singularidades", era común en relatividad general. Estos eran los modelos cerrados de Friedman (1922) y la solución de Sitter. Friedman, buscó las soluciones con la forma:

ds2 = −F dt2 + a2 (t) (dχ2 + sin2 χdΩ2)

Donde a(t) es una función de tiempo t, F es una función arbitraria, y dΩ2 representa la métrica estándar para una esfera redonda de unidad de radio.

En 1927, el sacerdote, matemático y cosmólogo Belga, Georges Lemaître construyó un modelo que combinaba los universos estáticos de Einstein y de Sitter, en el sentido de que este se acercaba al primero en distantes tiempos pasados y al último, en tiempos distantes futuros. De esta forma, el dio una explicación para el corrimiento hacia el rojo de las nebulosas (galaxias), basadas en la relatividad general.

Luego, en un prominente y relevante trabajo (213) construyó una solución general a las ecuaciones de campo (conocida actualmente como Modelo Lemaître-Tolman) encontrando resultados muy interesantes, incluyendo la inestabilidad del universo estático de Einstein, en particular, una singularidad inicial de tipo tiempo-creación de Friedman para modelos expansivos, capaz de explicar los corrimientos al rojo cosmológicos observados.

El Teorema de 1965: Sus implicaciones y relevancia.

Penrose buscaba demostrar que las desviaciones de simetrías esféricas no eran capaces de prevenir la formación de singularidades, como las descritas en el Colapso Oppenheimer-Snyder, en el marco de la relatividad general. Recordar que esto fue un trabajo de un resultado previo por Lemaître, pero era necesaria una cantidad de simetría (homogeneidad espacial). 

Para alcanzar esta meta, Penrose tomó la idea de incompletitud para describir espacio-tiempo singular, e introdujo la noción de superficie cerrada y atrapada por primera vez; una mayor contribución conceptual a la física del campo gravitacional. En lo que sigue, tenemos una versión moderna del teorema de Penrose:

Teorema 2 (Teorema de la Singularidad de Penrose): Si el espacio-tiempo contiene una hipersuperficie no-compacta Cauchy Σ, y una superficie cerrada y atrapada, y si la condición de convergencia tiene un uµ nulo, entonces existen geodésicas nulas incompletas.

Una hipersuperficie Cauchy es un "instante de tiempo" que provee buenos valores de condiciones iniciales para el espacio-tiempo entero. Más precisamente, es una hipersuperficie acronal, la cual es encontrada una vez y sólo una vez por todas las curvas causales sin fin.

Pero, ¿qué es una Singularidad?

El problema de cómo definir una singularidad en Relatividad General fue difícil, de hecho. Intuitivamente, esperamos que las divergencias de cualquier cantidad física o geométrica, pueda ser un detalle característico de las singularidades. Sin embargo, existen problemas de varios tipos:

1) Las singularidades no pertenecen al espacio-tiempo, la cual esta por definición, constituida de puntos regulares.

2) Incluso, si uno usa sólo curvaturas invariantes, independientes de la base, esta puede llevar a que todas estas desaparezcan y sigan existiendo singularidades.

3) Algunas veces, las singularidades surgen debido a malas propiedades del bulto tangente, por instancia, en singularidades cónicas, el principal problema es una falta de direcciones tangentes independientes.

4) Existen otros conocidos, más patológicos, ejemplos de espacio-tiempos con curvaturas desvanecientes y geodésicas incompletas.

5) Algunas veces, aparecen singularidades direccionales, definidas como puntos limites hacia la cual, el tensor de curvatura fluye a lo largo de algo, pero no a lo largo de otras, direcciones.

Siempre directo y conciso en sus afirmaciones: Durante una entrevista sobre el Big Bang, a traves de Radio 4 BBC, de Londres, el 25 de septiembre de 2010, Penrose dice: “No soy un creyente. No creo en religiones establecidas de ninguna clase. Puedo decirles que soy un ateísta”

Estas complicaciones llevan a elaborar una clasificación de posibles singularidades surgiendo de la curvatura de los tensores. En lenguaje llano y simple, una singularidad representa un punto del espacio-tiempo, en el cual la curvatura del espacio-tiempo se hace infinita. Lo estipulado por el teorema de las singularidades es que tiene que existir una singularidad en determinadas circunstancias, en particular, que el Universo tuvo que haberse iniciado con una singularidad.

Después de 1965: El impacto inmediato del teorema.

El teorema de la singularidad de Penrose impacto a la comunidad relativista. Su impacto fue amplio, profundo y directo. Unos pocos meses después de ser publicado, Hawking mostró que superficies atrapadas, en su versión pasada, estarán presente en cualquier universo en expansión, cerradas a ser espacialmente homogéneos e isotrópicos. 

"Estoy agradecido de estar aqui para celebrar el cumpleaños de Roger... Como muchas personas, encuentro dificil de creer que el tenga 65. Solo espero que yo este en tan buena forma cuando alcance esa edad"

Stephen W. Hawking.

Catedrático Lucasiano de Matemáticas de la Universidad de Cambridge, Departamento de Física Teórica y Matemática Aplicada de la Universidad de Cambridge, Silver Street, Cambridge, Inglaterra.

Con motivo de los 65 años de Roger Penrose condensado en el libro "The Geometric Universe: Science, Geometry and the work of Roger Penrose, de 1988.

Hawking desarrollo nuevas ideas, la cual, a pesar de algunas imprecisiones iniciales, cuando se combino con lo previsto en el trabajo de Penrose, formó el núcleo de los  modernos teoremas de las singularidades. 

Otra importante ramificación de las ideas detrás del teorema de las singularidades fue el estándar para la teoría de los agujeros negros. Todo comenzó con otro gran trabajo de Penrose (245) donde fecunda la idea del infinito conformal, llevando a una definición (débil) plano asintótico, y por ende, a la noción del horizonte de eventos. 

El resultado Hawking-Penrose, se basa en las observaciones fundamentales que, en tres aspectos, son incompatibles:

- Cada geodésica causal sin final tiene puntos conjugados.

- No existen curvas de tiempo cerradas.

- Existe un set en la que el futuro (o pasado) tiene una frontera compacta.

Estos últimos sets son llamados "sets atrapados", en la literatura, pero estos no deben ser confundidos las superficies atrapadas. El concepto de superficie atrapada es local; allí no existe la necesidad de conocer la estructura de su futuro o pasado.

Efectos Cuánticos.

Una línea muy importante de investigación surge de la tensión entre los teoremas de las singularidades y la (aun no encontrada) teoría cuántica de la gravedad. Es ampliamente aceptada que la existencia de singularidades clásicas señalan un rompimiento de la teoría clásica en condiciones extremas, lo cual es precisamente cuando los efectos cuánticos gravitacionales llegan a ser relevantes.

Stephen Hawking y Roger Penrose. A juicio del autor, es posiblemente, el dúo científico de más renombre en el siglo XX y uno de los mejores de la historia. Sus aportes y teorías, en el campo de la Cosmología y la Relatividad, marcaron un rumbo que ellos mismos trazaron. Así como Einstein aprendió de Marcel Grossman la geometría de Riemann, del mismo modo Hawking aprendió de Penrose las técnicas topológicas de las teorías de las singularidades, aplicables a los agujeros negros; dichas herramientas analíticas las aplica Hawking para su tesis doctoral, para así, ubicarse en el corazón de la física teórica convencional. Además de ello, Penrose sería uno de los miembros del comité de revisión de la tesis de Hawking, en 1965.

Por ello, existe una necesidad de clarificar si los teoremas de las singularidades, o parte de esta, pueden sobrevivir cuando entre en el régimen cuántico, o si ella simplemente se desvanecerá del todo. Un primer paso hacia el análisis de los teoremas de las singularidades en este aspecto, es el debilitamiento de las "condiciones de energía", también relevante en el régimen clásico, esto es, encontrar una versión apropiada de la condición de curvatura en los teoremas.

¿Son los teoremas de las singularidades algo del pasado? La respuesta a esta pregunta es un categórico "no". El tema ha evolucionado a nuevas versiones, o nuevos tipos, de teoremas de singularidades que estan siendo construidos para tomar en cuenta recientes aspectos físicos tales como, teorías de altas dimensiones, una (positiva) constante cosmológica, efectos cuánticos, inflación, entre otros.    

Penrose: Una leyenda viva.

        En la actualidad, Penrose es ampliamente reconocido en el ámbito científico como uno de los matemáticos más importantes y exitosos del siglo XX. Sus trabajos sobre Cosmología y la Teoría de la Relatividad General, son considerados por los expertos, la segunda más importante después de Einstein, lo que nos dice inequívocamente, el papel desempeñado en su estudio.

        Los honores, méritos, premios, posiciones y trabajos hablan por sí mismo. Es Profesor Emérito Rouse Ball de Matemática de la Universidad de Oxford, Profesor Distinguido Francis y Helen Pentz de Física y Matemática, de la Universidad Estatal de Pennsilvania, además de ser elegido Fellow de la Sociedad Real de Londres, en 1972, Asociado Extranjero de la Academia Nacional de Ciencias de los Estados Unidos en 1988. Además de ello, fue nombrado caballero, en 1994.

Sir Roger Penrose, sustentador de la Teoría de la Cosmología Cíclica Conforme, entre otras, durante en el Festival della Scienza, Génova, 2011.

Entre los grados honorarios obtenidos tenemos la de la Universidad de Brunswick (1992), Universidad de Surrey (1993), Universidad de Bath (1994), Universidad de Londres (1995), Universidad de Glasgow (1996), Universidad de Essex (1996), Universidad St Andrews (1997), Universidad de Santiniketon (1998), Universidad de Varsovia (2005), Universidad Católica de Lovaina (2005), y la Universidad de York (2006).   

_________________________________________________________________________

Referencias y Recursos consultados:

A. Vilenkin and A. C. Wall, “Cosmological singularity theorems and black holes,” Phys. Rev. D89 no. 6, (2014) 064035, arXiv:1312.3956 [gr-qc].

G. J. Galloway and R. Schoen, “A Generalization of Hawking’s black hole topology theorem to higher dimensions,” Commun. Math. Phys. 266 (2006) 571–576, arXiv:gr-qc/0509107 [gr-qc].

P. T. Chru´sciel, G. J. Galloway, and E. Ling, “Weakly trapped surfaces in asymptotically de Sitter spacetimes,” Class. Quant. Grav. 35 no. 13, (2018) 135001, arXiv:1803.02339

Kahn, J. and Markovic, V., “Immersing almost geodesic surfaces in a closed hyperbolic three manifold,” ArXiv e-prints (2009), arXiv:0910.5501

(213) Lemaître, G. 1933 L’Univers en expansion. Ann. Soc. Sci. Bruxelles, A53, 51; English translation reprinted as a Golden Oldie 1997 Gen. Rel. Grav. 29, 641.

[248] Penrose, R. 1965: Gravitational collapse and space-time singularities. Physical Review Letters. 14, 5.

Roger Penrose, "Asymptotic Properties of Fields and Space-Times", Physical Review Letters 10, no. 2 (1963): 66–68. (en ingles).

Einstein, A. 1941 Demostracion de la no existencia de campos gravitacionales sin singularidades de masa total no nula Revista de la Universidad Nacional de Tucuman A2 5–10: English translation: Revista de la Universidad Nacional de Tucuman A2 11-16.

Hawking, S. W. and Ellis, G. F. R. 1973 The large scale structure of space-time, (Cambridge Univ. Press, Cambridge).

Hawking, S. W. and Penrose, R. 1970 The singularities of gravitational collapse and cosmology Proc. Roy. Soc. London A314, 529.

Mario Livio, “Searching for Golden Ratio”, Astronomy, abril 2003, vol 31-nr 04, page 52-57.

Jerjen, H. 2007 Cosmological singularity theorems and spatial averages, Diploma thesis (University of Neuchˆatel, Switzerland). Available online: http://www.unine.ch/phys/string/JerjenThesis.pdf (en ingles).

Wald, R. M. 1998 Gravitational collapse and cosmic censorship, in Black Holes, Gravitational Radiation and the Universe. edited by B.R. Iyer and B. Bhawal (Springer, Berlin) arXiv: grqc/9710068 (en ingles).

Jose, M. M. Senovilla, David Garfinkle, The 1965 Penrose singularity theorem, Fısica Teorica, Universidad del Paıs Vasco, Apartado 644, 48080 Bilbao, Spain,  Dept. of Physics, Oakland University, Rochester, MI 48309, USA and Michigan Center for Theoretical Physics, Randall Laboratory of Physics, University of Michigan, Ann Arbor, MI 48109-1120, USA. arXiv:1410.5226v2 PACS numbers: 02.40.Dw, 04.20.Cv, 04.20.Gz (en ingles).

R.-G. Cai, L.-M. Cao, and Y.-P. Hu, Classical and Quantum Gravity 26, 155018 (2009), arXiv:0809.1554

D. An, K. A. Meissner, P. Nurowski, and R. Penrose, “Apparent evidence for Hawking points in the CMB sky,” (2018), arXiv:1808.01740 [astro-ph.CO].